Multiphysics

 

Introduction

Dr. Liu authored the first comprehensive multiphysics book, which coveres the necessary mathematics, physics, application, and implementation of multiphysics. In addition, LiuRG has been leading the development of the first website for the general learning and networking of multiphysics: multiphysics.us. Please visit multiphysics.us if you want to learn more about multiphysics. The following gives out very brief information regarding some multiphysics work that has been conducted by LiuRG.

 

 

Background

Multiphysics treats simulations that involve multiple physical models or multiple simultaneous physical phenomena. For example, combining chemical kinetics and fluid mechanics or combining finite elements with molecular dynamics. Multiphysics typically involves solving coupled systems of partial differential equations. Many physical simulations involve coupled systems, such as electric and magnetic fields for electromagnetism, pressure and velocity for sound, or the real and the imaginary part of the quantum mechanical wave function. Another case is the mean field approximation for the electronic structure of atoms, where the electric field and the electron wave functions are coupled. Here a field denotes a physical quantity that has a value for each point in space and time.

Multiphysics is not a straightforward of superposition of multiple physical fields. Typical physical fields include gravitational field, heat transfer, particle transport, groundwater movement, stress and strain field, electrostatics,, magnetostatics, wave propagation, and quantum mechanics; and in a broader scope, also include chemical kinetics. Some of these fields are coupled in nature and cannot be separated without sacrifying the accuracy of the analysis significantly, such as hydrodynamics. For some multiphysical problems, such as electromagnetic processes, it would be meaningless to separate them. The widespread existence of multiphysical phenomenon can manifest itself as significantly different states from conjoined twins to loose alliances. What dramatically increase the complexity of multiphysics are the high nonlinearity in material properties and geometries and their interwoven connections with different fields. This makes each multiphysical problem a unique object and makes it extremely hard to understand the nature of the problem.

 

Framework for Thermo-Hydro-Mechanical Processes in Porous Materials

In past few years, a theoretical framework has been established and tested for the thermo-hydro-mechanical processes in porous materials (Liu and Xiong, 2012; Liu et al., 2012a; 2012b; Liu et al., 2013). Porous materials include multiple phases and species, which make them a perfect seedbed for multiphysical processes. Within all these processes, the thermo-hydro-mechanical processes are believed to be a typical and predominant one. The three types of physical fields, i.e., thermal, hydrological/hydraulic, and mechanical fields, all fall into the scope of conservation problems which can trace back to continuum mechanics. A abbreviated and general description of the framework is as follows. Let leave all assumptions in mathematics and physics such as the representative elementary volume and start from the balance equation:

\[ \frac{\partial u}{\partial t}=\nabla \cdot [u(\mathbf{v_{\partial \Omega}}-\mathbf{v})] + \nabla \cdot \mathbf{q} + \mathbf{h}\].

In porous materials, the governing equations for the thermal, hydrologic/hydraulic, and mechanical field can be derived based on the above equation according to the conservation of mass, energy and momentum:

\[ \frac {\partial {\rho_j \theta_j}}{\partial t} =-\nabla \cdot (\rho_j \theta_j \mathbf{v}_j) + \dot{m}_j\]

\[ \frac {\partial {\rho_j \theta_j \mathbf{v}_j}}{\partial t} =-\nabla \cdot (\rho_j \theta_j \mathbf{v}_j \mathbf{v}_j) + F_j \]

\[ \frac {\partial {\rho_j e_j}}{\partial t} =-\nabla \cdot (\rho_j e_j \mathbf{v}_j) + \dot{e}_j^T\]

For specific problems, the above equations can be eventually formulated into extended forms of Fourier's equation, Richards' equation/Groundwater equation, and Navier's equation. The subscript \(j\) denotes different species or phases. Therefore, for a multiphase and multicomponent system, the number of governing equation could be increase manyfold.

The above framework has been tested against applications such as soil freezing, cement hydration, gas hydrate dissociation. More applications such as sanitary landfills, geothermal applications, gas recovery, and carbon sequestration are also sought.

 

Mathematical Algorithms for Ensuring Physical Meaning of Quantities

Engineering applications such as multiphysics simulations focus on modeling physical processes based on mathematical descriptions of these processes. The underlying assumption is that the mathematical descriptions should approximate the natural mechanisms so that the simulation results will approach the true solution. This is usually not a big problem in traditional simulations as there is only one single physical process, in which the relationships between quantities are usually relatively obvious and simple. However, in multiphysics, one big problem is that different fields are tangled together and it is possible that quantities from different physical fields are dependent on each other in a very obscure and highly nonlinear way. For a multiphysical problem, one research group may need to start from both the physical and mathematical aspects for establishing a model. A considerable amount of time is needed for establishing such a model and solving it using numerical techniques. However, it is less common for engineers to work with mathematician especially for the establishment of model. For example, general purpose solvers or schemes may be used to discretize and solve a problem. These could cause a major issue as the physical and mathematical descriptions are not fully related, leading to failures in formulating the problem. In this case, the modelers may find it is very difficult to find a convergent solution or the simulation can hardly approach the true solution even if unrealistic values are tried for all the parameters in a trial and error basis. One common outcome is that the values of some parameters will violate physical rules. One typical example is that the volumetric water content could exceed the porosity of the porous material or reduce to a negative value.
The next step is to construct physically relevant numerical approximations. In mathematical language, some target quantities may have bounds. For example, the exact solution of a scalar hyperbolic conservation equation or a parabolic equation satisfies a maximum principle (MP); some physical quantities, such as density and energy, cannot be negative, etc. In practice, numerical approximations can easily be out of the bounds even though the exact solution is smooth. Especially, negative numerical density is totally unacceptable. Most of the numerical solvers in multiphysics problems are based on the traditional FEM, where continuous piecewise polynomials are constructed to approximate the exact solution. Such methods can hardly preserve the bounds as we want, and most of the research focuses on Maximum Principle (MP) satisfying schemes which have been studied for more than 30 years. Most of the schemes require linear approximations (e.g. Farrago, 2005, 2006; Vejchodsky, 2010). Therefore, the schemes are at most second order accurate. Moreover, some special requirements for the meshes may also be necessary. For example, the rectangular mesh cannot be narrow, i.e. the longer edge is not greater than \(\sqrt{2}\) times the shorter one; the triangles should be in good shape, i.e. the interior angles cannot be greater than \(\pi/2\). Recently, a MP preserving FEM for scalar conservation equations has been constructed (Guermond, 2014). The method does not require acute triangles. However, the scheme is designed by adding a first-order artificial viscosity. Therefore, the scheme is only first order accurate. Moreover, we believe that the construction of high-order schemes is not easily extendable. In practice, the geometry of the domain might be very complicated, and we want the meshes to be relatively coarse. Therefore, we have to seek a new numerical method, which is high-order accurate and can preserve the bounds for arbitrary meshes. Therefore, we have been looking for new techniques such as bound-preserving (BP) technique, to make the numerical approximations to be physically relevant. We have been working a partner group from mathematics, Dr. Yang Yang's Group at Michigan Tech, to seek the solutions.

 

Couplings between Physical Fields

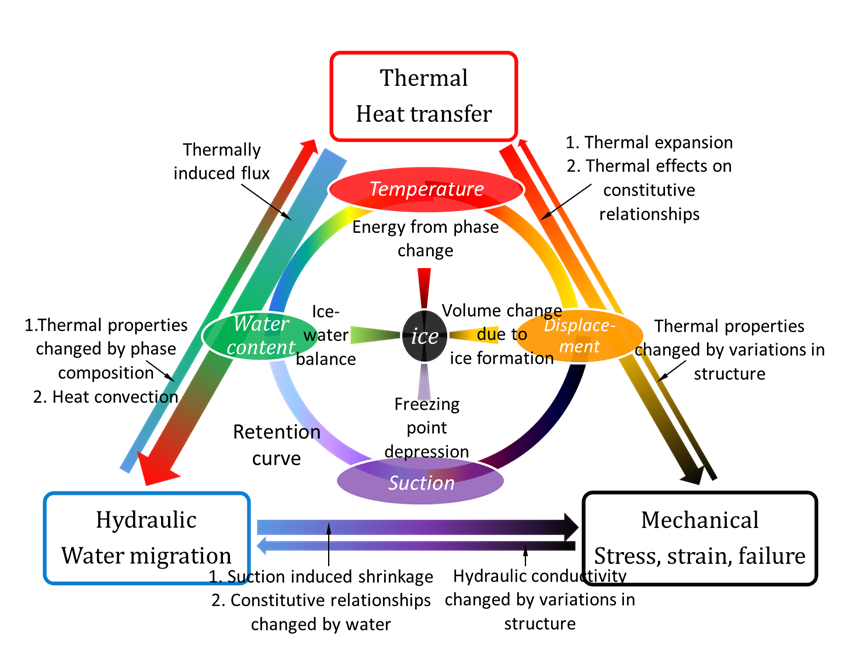
The couplings between different physical fields, as shown in the following figure, could be very complicated. Taking a typical thermo-hydro-mechanical problem in soils for example, many phenomena are triggered by a change in the thermal field. This change in thermal field serves as an excitation, similar to an external force in mechanical field, and gives rise to changes to the whole system in terms of a multiphysical process. For example, thermal changes can alter the compressibility and shear strength (mechanical) of a porous material, induce water migration, and change hydraulic properties (hydraulic). These are the typical couplings from the thermal field to mechanical and hydraulic fields, respectively. These changes in mechanical and hydraulic fields will in return exert 'reacting forces' to the thermal field. For example, heat transfer can be promoted by energy convected by migratory water, and thermal properties such as heat capacity and thermal conductivity can be changed due to the variations in the structure and composition of soils. The 'reacting forces' represent the couplings from the other two physical processes to thermal field. It is worthwhile to point out that the couplings from thermal field to other fields are usually strong couplings. Among these couplings, some could be relatively strong such as the thermally induced water flux. This is because it could be the dominant in the hydraulic field and cause significant changes in the mechanical field. For couplings like this, it is extremely important to handle them in a way close to their physical state. Otherwise, unexpected oscillations or violations in conservation laws will occur. To better account for the couplings in multiphysics, it is proposed that couplings are categorized into two major types. The first type of coupling is system couplings. For this type, one governing equation will contain dependent variable (s) of another governing equation(s). In that way, different equations are coupled as a “system”. For this type, usually the oscillations caused by discontinuities or big gradients in the solution could be a problem. The second type of coupling, a parameter in the equation is a function of other parameters or dependent variables. For this type of coupling, the high non-linearity of such a parameter could cause major difficulty in solution. The couplings are categorized in this way because these two types are usually treated in a different way in discretization due to their distinct nature. Development of algorithms for dealing with these two types of couplings are currently undertaken.